无绝缘高温超导磁体电-热-磁混合模型的原理与计算过程

本混合模型针对的对象是使用REBCO超导带材的，以双饼为基本结构的无绝缘超导磁体。

模型内部的电流电压状态、温度状态和磁场状态三者相互耦合，能够展现磁体各个时刻的电-热-磁状态。

模型在时间上和空间上都是离散的，时间步长没有下限也没有上限，空间步长则受限于计算机的机能。

模型建立的目标是用来展现磁体在励磁过程中、临近失超的状态；在时间步长足够小的情况下，模型也能用来仿真磁体失超过程；对预测磁体实际性能、判断磁体运行状态和失超保护都能起到很大的作用。

1. 超导带材模型

超导带材模型的构建是整个TME模型构建的基础，因为它提供了基础的电感、电阻、临界电流和传热特性；这些特性直接影响整个磁体的电流和温度分布————这两种分布是研究磁体运行过程的核心要点。

1.1 带材结构

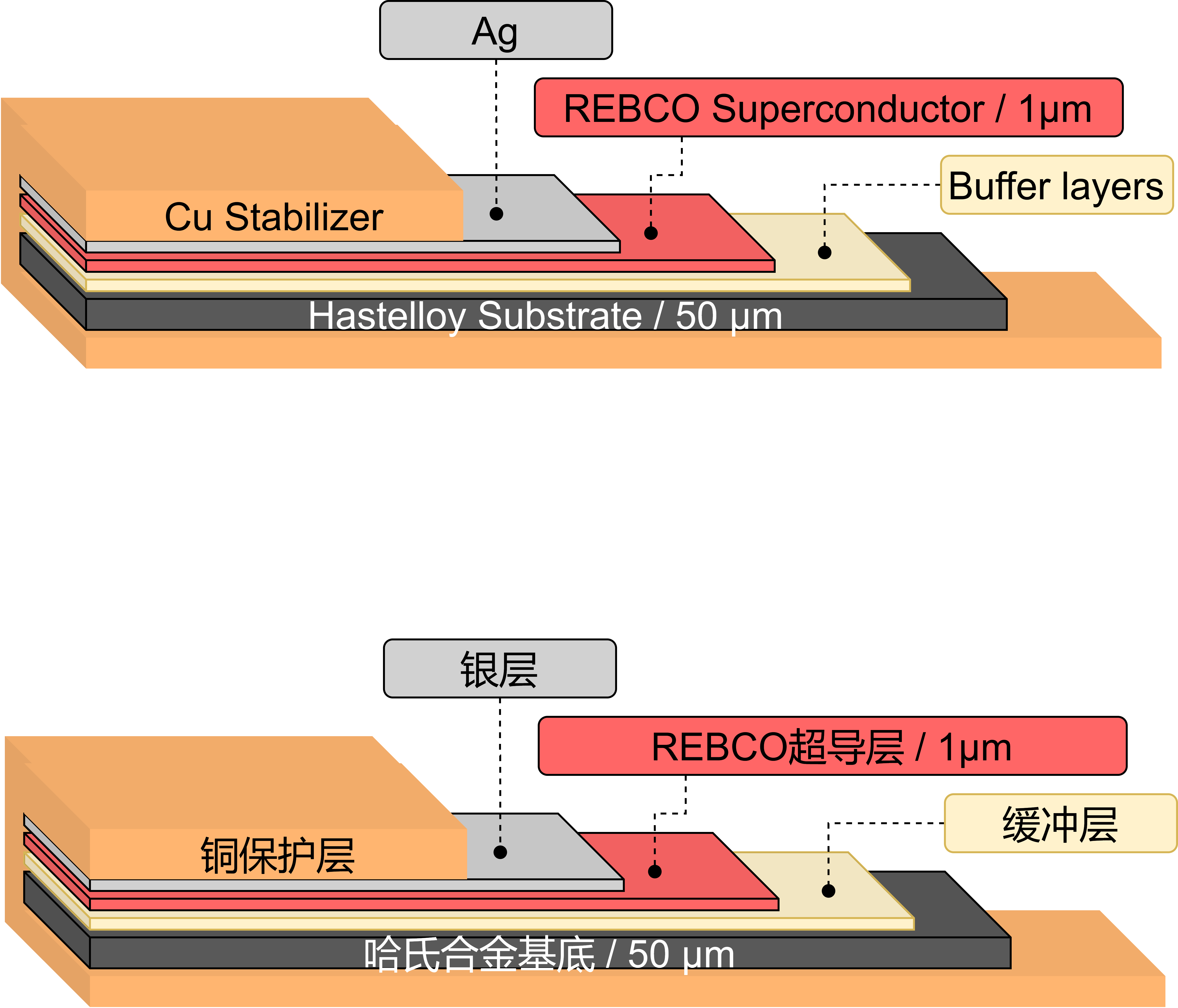
REBCO截面图 REBCO三维图

REBCO带材主要由基底、超导层和保护层三个部分组成：

基底的成分是哈氏合金/镍合金/Hastelloy，物理性能优秀，是超导层沉积的基底，也是带材整体强度的主要来源；
超导层虽然厚度只占整个带材厚度的1%/1μm，但在工作过程中却是电流的主要路径————REBCO材料本身的可以承受电流密度非常巨大，在工程应用中，制约磁体性能的并非通过电流能力，而是磁体内部的结构强度；
保护层成分复杂，主要组成是铜，一方面最外侧的保护层影响了带材的接触电阻、接触热阻等特性，另一方面，包裹整个带材的铜层也是磁体运行过程中沿法向穿过整个带材的电流的主要路径。

1.2 临界电流

带材的临界电流数据来源于两种参数，一种是厂家给出的临界电流，另外一种是双饼绕制之后液氮测试获取的临界电流数据。

从仿真的角度上来说，单纯的临界电流数据，采用第二种实测的临界电流当然会更加接近仿真结果；但是另一方面，临界电流随温度和磁场的变化趋势非得使用由厂商给出的不同磁场和温度下的临界电流数据进行拟合不可。

B	Ic
1	55
2	29
4	8.5
6	1.8
6.4	1

那么临界电流与垂直磁场之间的关系：

I_{c} = I_{c0}*e^{-0.73\times B}

T	Ic
4.2	1800
10	1400
20	1100
30	845
65	200
77.3	55

那么临界电流与温度之间的关系：

I_{c} = I_{c0}*e^{-0.04\times T}

绝对零度 -273.15°C = 0K 液氮温度 -196.56°C = 76.59Ks

I_{cB,T} = I_{c76.59}\times e^{-0.73B}\times e^{-0.04(T - 76.59)}

1.3 传热参数

带材的传热参数需要视不同的情况考虑：

在顺着带材延申的方向上，传热方式为固体传热，热阻为带材本身的热阻，由构成带材的不同材料的热阻加权平均得到（操作中使用铜的热阻），同时会受到环境温度的影响。
在带材与带材的接触面上，传热方式为固-固传热，热阻为接触热阻，与接触面的材质、接触面的粗糙程度、环境温度和接触面应力相关（操作中使用接触热阻固定值）。
在带材与环境的接触面上，传热方式为固液传热，但是考虑到接触效率和发热功率，基本可以认为接触面温度不变。

1.4 电阻参数

顺着带材延申方向的电阻与带材的长度成正比，也取决于带材的临界电流、垂直磁场和温度等参数。从原理上来说，垂直磁场和温度对于实际临界电流的影响也体现在电阻上。

而在带材厚度的方向上，带材的电阻率则于带材的长度成反比，另外取决于构成超导带材的材质、接触面状态和接触应力等参数。在实际操作中，一般在绕制双饼之后，通过双饼在低电流下的时间常数计算双饼总的径向电流；从而获得电阻率数据。

$R_{c}=C \times l \times \frac{I^{n-1}}{I_{c}^{n}}$

2. lv.1模型

lv.1模型描述的是一个匝数为T的单饼线圈，将这个单饼线圈的每一匝分解为A个元素；通过分析每个元素在每一个时间点的的电流、温度和磁场之间的耦合关系，就可以获取单饼中任意位置和任意时间的电流、温度和磁场状态。

螺旋单饼

利用抽象模型的各项参数可以构建方程，解方程即可获取模型中的各项状态。

计算流程框图

在时间尺度上，采用迭代的方式对各个时间点的电路模型进行耦合，而磁场和温度场在时间尺度上不进行耦合，在迭代过程中只传输电流数据。

2.1 电路方程

电路模型


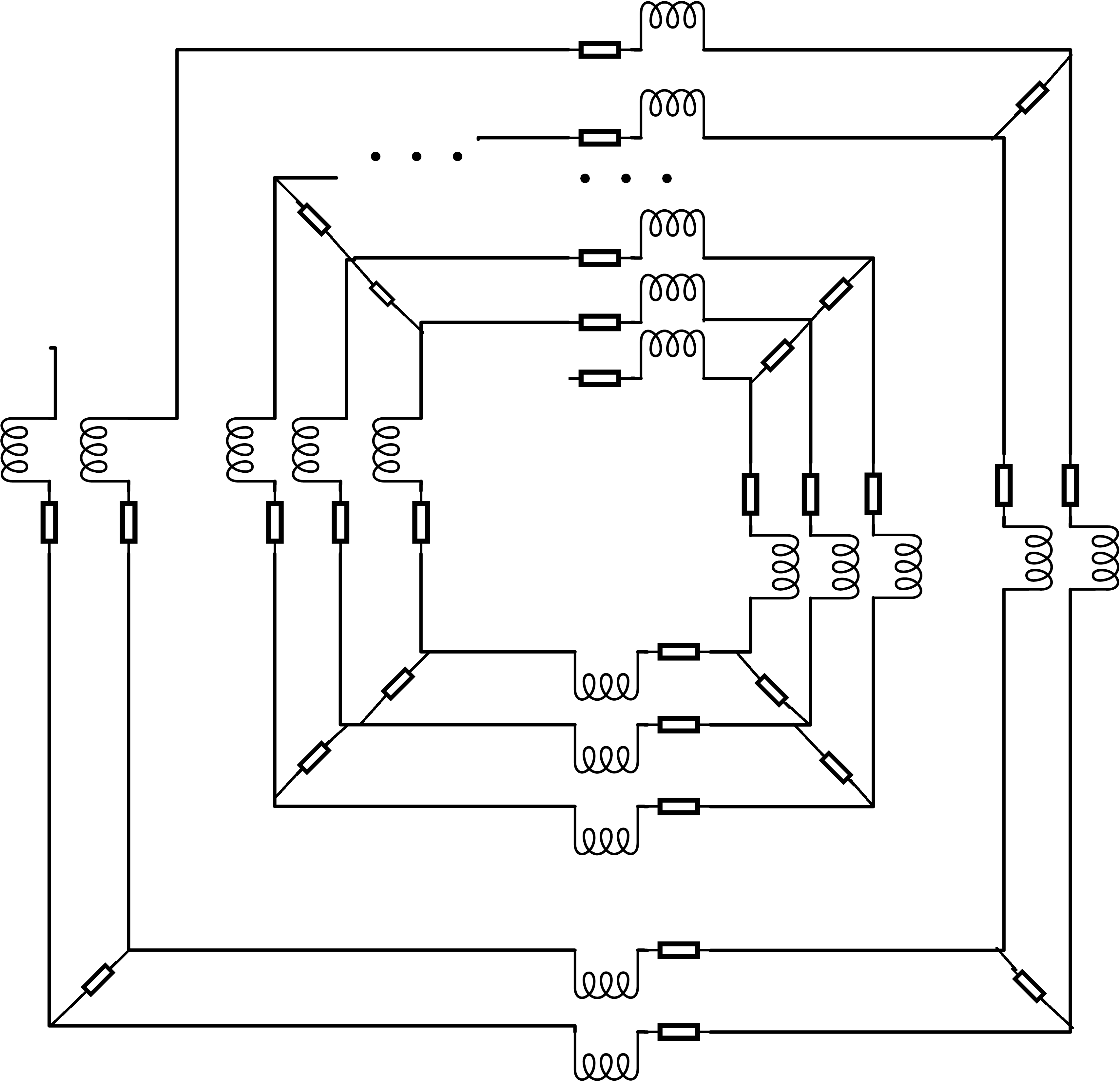
xxxxxxxxxx
b(此模型还要添加文字才能使用)

在任意时间点，运用基尔霍夫定律解这个电路，可以得到每个节点之间电路的电流，即各个位置的环向电流和径向电流。对于一个划分好电路网格，节点数

{N} = {N_{t}}\times{N_{a}}

${N_{t}}$ ${N_{a}}$ 表示每一匝的节点数目。

2.1.1 电流方程

基尔霍夫电流方程

对于每一个节点可以列出一个基尔霍夫电流方程：

{i_k} - {i_{k + 1}}{\text{ + }}{j_{k{\text{ - }}{n_e}}} - {j_k} = 0;

而对于最内匝、最外匝的节点，电路结构稍有减少，可以列出一个包含N个方程的基尔霍夫电流方程组：

\left\{\begin{array}{ll} i_{k}-i_{k+1}-j_{k}=0 ; & k \in\left[1, n_{a}\right] \\ i_{k}-i_{k+1}+j_{k-n_{e}}-j_{k}=0 ; & k \in\left[n_{a}+1, N-n_{a}\right] \\ i_{k}-i_{k+1}+j_{k-n_{e}}=0 ; & k \in\left[N-n_{a}+1, N-1\right] \\ i_{k}+j_{k-n_{e}}=I_{O P} ; & k=N \end{array}\right.

2.1.2 电压方程

电压方程元素

${R_{k}}$ 为核心，可以构建以环路为元素的电压方程：

\sum\limits_{m = k}^{k + {n_a} + 1} {(\sum\limits_{n = 1}^{N} {{M_{m,n}}\frac{{d{i_n}}}{{dt}}} + {i_m}{R_{c,m}}}) - {j_k}{R_{r,k}} = 0;

${N-n_a}$ ${k>1}$ ${u_k} - {u_{k + {n_a}}} - {j_{k - 1}}{R_{r,k - 1}} + {j_k}{R_{r,k}} = 0$ ${u_k}$ 表示总电压：

{u_k}=\sum\limits_{m = 1}^{N} {{M_{k,m}}\frac{{d{i_m}}}{{dt}}} + {i_k}{R_{c,k}}

${M_{m,n}}$ ${R_c}$ ${R_r}$ 为径向电阻。

2.2 电感

lv.1模型中，需要计算空间中任意两个圆弧段的线段的电感，在没有明确的环状电流路径的情况下，采用矢量磁位的方式计算互感。另一方面，带材的宽度在lv.1模型的尺度上是必须考虑的，为了减小误差采用莱尔定律(Lyle method)对导线的宽度Width进行等效。

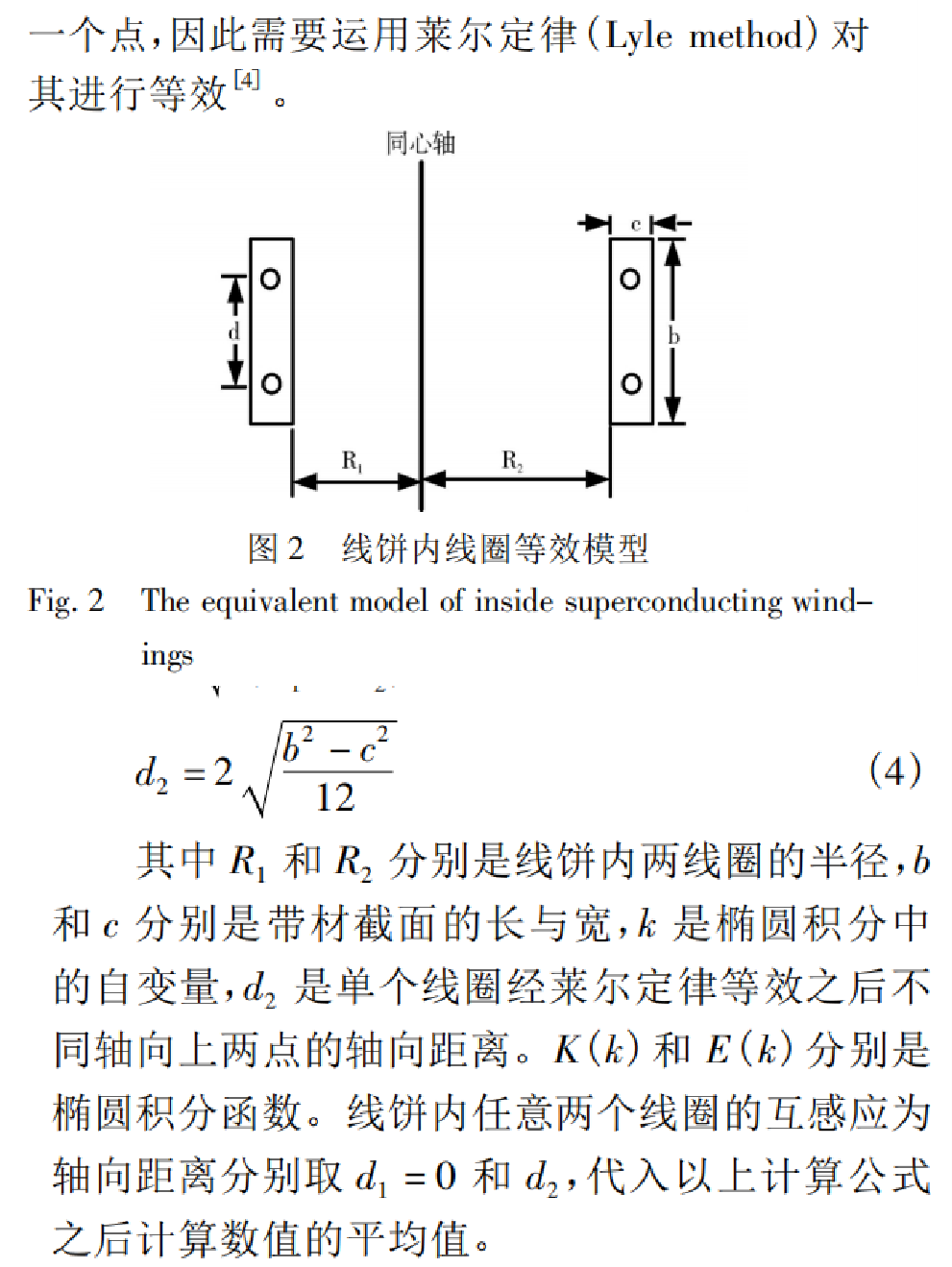
2.3 径向电阻

$ρ$ 的获取采用实验方式：对绕制的实验线圈进行小电流的断电实验，获取时间常数，线圈的电感由线圈的结构决定。

实验线圈对策电感值为0.025143061116848 H；时间常数为55.2 s

径向电阻率

\rho = 6.546178680702746\times {10}^{-10} {{\Omega} \cdot {{m}^{2}}}

各个面的接触面积与径向电阻率的值结合起来就可以得到径向电阻。

2.4 环向电阻

从原理上来说，环向电阻为超导路径电阻与非超导路径电阻的并联：

R_c=\frac{R_{sc} \cdot R_{nc}}{R_{sc}+R_{nc}}

但是在一般情况下，超导路径的电阻比非超导路径的电阻值小数个数量级，故在仿真模型中认为环向电阻的值就是超导路径的电阻值。

而超导带材的电阻可以用下列的公式来表达：

R_c = {C_r} \cdot l \cdot {\frac{{I}^{n - 1}}{{I_c}^n}}

${I_c}$ ${I}$ ${n}$ ${C_r}$ ${I_c}$ ${10uV/m}$ ${l}$ 为线段长度。

如果知道电流线段的临界电流，就能够结合实际电流求出其环向电阻。带材的临界电流受带材所处的温度和垂直磁场的影响：

{I_c} = {I_{c0}} \cdot {e^{{C_B} \cdot B}} \cdot {e^{{C_T} \cdot (T - {T_0})}}

2.6 温度

由于超导磁体单饼各个元素的热容很小而热导率很大，所以近似的认为模型中任意一点任意时刻的都处于热平衡的状态，即发热量与散热量相等，而每一点本身的温度与自身的散热量息息相关，从而可以获得传热平衡方程。

Q = P

一个节点产生的全部热量等于其向外的全部传热。

一个节点产生的全部热量为：

P={{I_c}^2} \cdot {R_c}+{{I_r}^2} \cdot {R_r}

一个节点向外的全部传热为：

Q = \sum\limits_{k = 1}^6 {\Delta {T_k} \cdot {\lambda _k}}

${k}$ $\Delta {T_k}$ $\lambda _k$ 表示节点六个接触面的导热系数，导热系数与接触面类型、材质、面积和传热距离等相关。

在已知每个节点电流的情况下可一得到每个节点的温度。

2.5 垂直磁场

垂直磁场的计算运用比奥萨菲定律：

$d \vec{B}=\frac{\mu_{0}}{4 \pi} \cdot \frac{I d l \times \vec{r}}{r^{3}}$

已知每个电流源的位置和电流，就可以求出空间任意位置的磁场值。

3. lv.2模型与双饼模型

lv.2模型对象为匝数为T的单饼，但将每一匝视为一个元素，描述其电流、磁场和温度状态。

3.1 lv.2模型

这是lv.2模型的电路模型，将每一匝线圈视作一个电流单元，径向电流和环向电流的和为控制电流，径向电阻和环向电阻分流。 lv.2模型的电路方程为：

\frac{{\Delta {i_k}}}{{\Delta t}} \cdot {L_k}{\text{ + }}{i_k} \cdot {R_{c,k}}{\text{ = }}{j_k} \cdot {R_{r,k}}

其中模型的自感计算和互感计算可以使用椭圆积分：

$k^{2}=\frac{4 a b}{c^{2}+(a+b)^{2}}<1$

$M=\mu_{0} \sqrt{a b}\left[\left(\frac{2}{k}-k\right) K-\frac{2}{k} E\right]$

${K}$ ${E}$ ${k^2}$ 对应的完全椭圆积分

径向电阻的计算可以参考lv.1 。环向电阻的计算则要考虑总的垂直磁场和温度，同样可以参考lv.1 。

3.2 双饼模型

通过lv.1模型和lv.2模型的组合就可以构建双饼模型，其中一个面采用lv.1模型，另外一面采用lv.2模型，能够同时实现快速计算和高精度仿真。

两种模型之间的耦合包括：电感耦合和磁场耦合

3.2.1 电感耦合

利用同轴圆环之间的电感，除以lv.1模型中每匝线圈的分析个数就能够得到耦合电感。

${M_{2,1}} = \frac{{{M_{2,1}}}}{A}$

3.2.2 磁场耦合

垂直磁场的计算运用比奥萨菲定律：

$d \vec{B}=\frac{\mu_{0}}{4 \pi} \frac{I d l \times \vec{r}}{r^{3}}$

已知每个电流源的位置和电流，就可以求出空间任意位置的磁场值。

4. lv.3模型与磁体模型

在lv.2模型的基础上进一步简化，可以将整个单饼视为一个元素，完全放弃研究其内部的电流分布，而专注于这个单饼对其他更精细模型的影响。这种模型本身的存在在仿真中几乎没有什么意义，但是将lv.3模型作为元素耦合进磁体模型当中就能够大大的加快计算速度。

4.1 lv.3模型

lv.3模型的方程为：

\frac{{\Delta {i_k}}}{{\Delta t}} \cdot {L_k}{\text{ + }}{i_k} \cdot {R_{c,k}}{\text{ = }}{j_k} \cdot {R_{r,k}}

其温度视为环境温度，磁场以模型最中心位置为基准计算。

4.2 磁体模型

通过lv.1、lv.2和lv.3模型的结合，可以构建整个磁体的仿真模型——将磁体的一个单饼描述为lv.1模型，部份单饼描述为lv.2模型，剩下的描述为lv.3模型。

主要考虑各个单饼模型之间的电感耦合，是各个匝之间电感耦合的和。

5. 双饼仿真与实测数据对比

建立双饼仿真模型之后，结合实际情况给出控制电流就可以仿真双饼的励磁、稳态、失超过程；结合实际的双饼液氮试验数据验证仿真模型。

5.1 双饼参数

带材参数：

项目	数值
厂家	Superpower
厚度	0.098
宽度	4.04
临界电流	150A
n值	31.9

双饼参数：

项目	数值
左饼匝数	333
右饼匝数	333
厚度	8.75mm
内径	42.5mm

控制电流：

\left\{\begin{array}{ll} i=0.53 \times t & t \leqslant 113.21\\ i=60 & t>113.21 \end{array}\right.

5.2 数据对比

断电实验仿真时间常数

断电实验，电流5A，数据文件record_20200517_183743.mat 模型为对称模型

项目	图案	说明
B0		B0 = 0.057397
B,V		走势正常
B时间常数		时间常数为59.8，比实测的54.5要大，这可能是因为径向电阻在精细模型中比在粗糙模型中的效果要更小一些
V时间常数		和B的时间常数一致

仿真实验1

仿真实验，电流I = 0.53t，数据文件record_20200517_211934.mat，模型为多尺度模型，dt = 0.25s，磁体时长250s

项目	图案	说明
控制电流		没错
总电压		仿真电压比实测值小，这与断电实验中时间常数更长的结果相符，可能需要将精细模型的径向电阻设计得更大才行
总磁场		磁场值明显倍数级的不对，应该是测量时的问题
分区电压
分区电流

仿真实验2

此时仿真的模型中，所有的径向电阻调整为原来的59.8/56，时间常数应当有相应的改变

数据文件为record_20200519_091521.mat，总计算时间

项目	图案	详情
控制电流		没错
电压		总的来说，修正径向电阻之后更接近实测值，但是在稳定部分还是有微妙的差别，等修正环向电阻之后再看看情况
磁场		也是更好了，这个差别应当是测量探头的系数不对造成的
分区电压		粗糙模型的分区电压反而下降了，这可能是互感导致的，也说明二者的平衡非常微妙
分区电流		二者的环向电流都有所上升

仿真实验3

record_20200529.mat 降低临界电流此时仿真的模型中，所有的径向电阻调整为原来的59.8/56，临界电流调整为51.019

项目	图案	详情
电压		比临界电流调整前强多了
磁场		另外做了一下归一化，
归一化磁场		有一点点偏差，但是主要问题应该是出在测量时的系数上面
分电压		讲道理不应该差别这么大的
分电流		中间一些匝数的电流非常一致，但是最外侧几匝的电流就不同，可能也是导致分电压不一致的原因吧，是由电路结构决定的

磁体任意位置的垂直磁场

5~100mm间距导致的平面磁场。数据文件名level_2_1_Vertical_Magnet_field_Matrix.mat 其中：level_2_1_Vertical_Magnet_field_Matrix_X代表在目标点位置产生的X方向磁场计算矩阵；level_2_1_Vertical_Magnet_field_Matrix_Y代表代表在目标点位置产生的Y方向磁场计算矩阵Y 使用方法为，取出距离对应的这一层矩阵，直接乘源电流列向量，即可得到目标点位置的X、Y磁场列向量，将两个列向量取勾股数即为垂直磁场

互感矩阵

数据文件名level_2_1_Mutual_inductance_Matrix.mat

6. 磁体仿真计算与实测数据对比

进行TME耦合模型建设的总计目标就是对磁体进行整体仿真，由于计算能力的限制，不可能对整个磁体进行面面俱到、时时关注的仿真，那么进行多空间尺度、多时间尺度的混合仿真就是有必要的。

本模型的优势就在于在空间尺度上是离散而可无限精细化的，而在时间尺度上也是离散而可无限精细化的，一种简单易行的策略是：将整个磁体在磁场特性上最为“脆弱”的部分用lv.1模型进行构建；在临近失超的时间位置上采用更小的时间尺度。

下面通过一组实测数据的对比验证针对整个磁体的仿真模型。

6.1 磁体参数

6.1.1 32.25T内插磁体的结构

32.25T内插磁体的结构如下：

外层磁体【帝俊】由36个单绕双饼构成，其中两端的6个双饼分别采用6mm、7mm和8mm宽的REBCO带材绕制而成，剩下的30个双饼由4mm宽的REBCO带材绕制而成；
内层磁体【太一】由24个双饼构成，全部由4mm宽的REBCO带材绕制，其中两端的4个双饼为双绕；中部4个为notch线圈。

磁体模型

6.1.2 磁体模型

在仿真过程当中，将磁体模型进行简化：

外层磁体全部简化为4mm宽的单绕双饼；
内层线圈忽视notch结构，忽视各个双饼的匝数差异；
【太一】最端部的一个单绕单饼【陆压】用lv.1模型描述；
【太一】其他的单绕单饼用lv.2模型描述，共39个；
【太一】端部的双绕双饼拆分为单饼用用lv.3模型描述，共8个；
【帝俊】的双饼拆分为单饼，用lv。3模型描述，共72个。

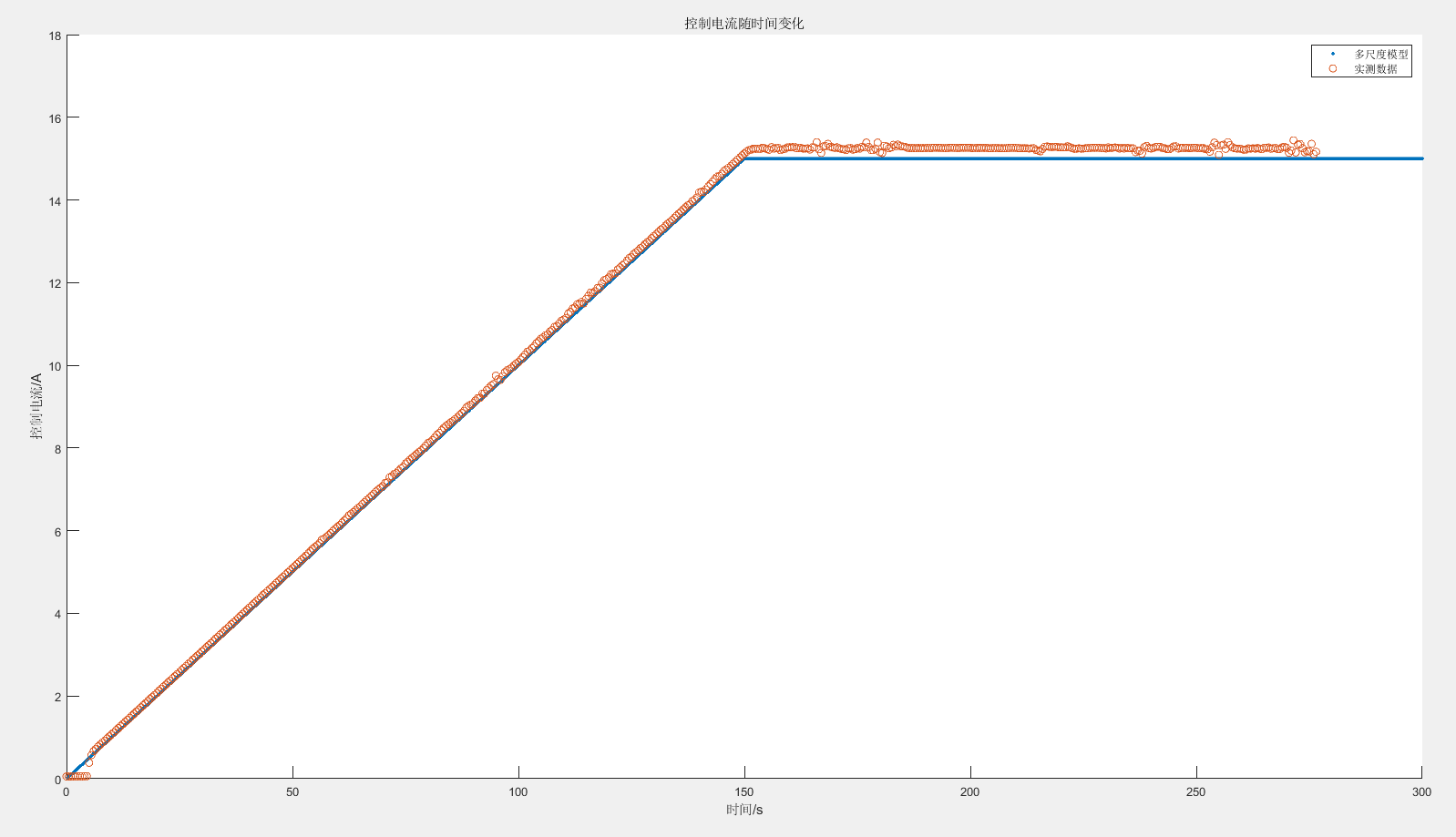
6.1.3 控制电流

$\left\{\begin{array}{ll} I=0.1 \times t & t \leq 15 s \\ I=15 & t>15 s \end{array}\right.$ 仿真中的控制电流采用了同样的方程。在实际测试中控制电流有三个特点：

初始阶段有电流跳变
稳定位置比设定的15A要稍高
在保持阶段电流不够稳定

6.1.4 散热条件

与双饼与液氮完全解除的良好散热环境不同，整个磁体的散热条件更为恶劣。对于每一个单饼而言，其上下两侧接触的不是液体环境，而是不同材质的隔板。只有内部与骨架接触的部分以及最外匝与绑扎接触的部分具有较为良好的散热环境。32.25T内插磁体中，双饼中间的隔板为经过处理的金属制，而两个双饼之间的隔板为环氧树脂（epoxy）材质。

仿真模型当中，将单饼上下两面的传热系数设置为0，即每个元素只能通过带材延申的方向以及带材之间接触的方向传热，而不能直接向环境传热：这种仿真条件能够更好的模拟励磁、运行和失超过程中的温升。

6.2 数据对比

项目	图像	说明
控制电流		15A
不同时间下环向电流由内向外的变化		可以看到环向电流的分布并不均匀
总电压		不同主要原因是开始阶段的电流突变
中心磁场		很接近
内磁体电压		和总电压类似
外磁体电压		和总电压情况相似