减小间距之后计算电流变化

多尺度模型数据处理

record_20200704_180641.mat lv1-lv2-lv3混合模型

项目	图像	说明
磁场
总电压
外电压
内电压

2020年7月6日07点29分

计算进度关注

A区计算情况：
D区计算情况：

单饼之间间距的统一

主要是二级模型之间；一级模型与二级模型之间的间距统一为
$$W+0.67 \times {10}^{-3}m$$

• 双饼垂直磁场 beta_Vertical_Magnet_field_Matrix.m
• 2-2垂直磁场 tool_level_2_2_Vertical_Field.m
• 双饼互感 tool_beta_Mutual_inductance_Matrix.m
• 2-1互感 tool_level_2_1_Mutual_inductance_Matrix.m A区
• 2-2互感 tool_level_2_2_Mutual_inductance_Matrix.m
• lv.2中心磁场 tool_level_2_Central_Magnet_field.m

2020年7月4日14点14分

数据处理

record_20200703_233341.mat lv1-lv2-lv3混合模型

项目	图像	说明
控制电流
总电压		一致
中心磁场
外磁体电压		没问题
内磁体电压		正常

数据处理

record_20200703_222342.mat lv2-lv3混合模型
实验数据:test_data_300.mat

项目	图像	说明
控制电流
总电压		实测电压比仿真电压大，可能是0~10s这一部分电流突变的影响，导致初始电压更高，而控制电流比设定值更高，导致电压更大，而且双饼之间还有非超导的桥接，会导致一些额外的电压升高
中心磁场
外磁体电压		没问题
内磁体电压		正常

实验数据的情况

1. 前面部分数据缺失
2. 电压数据波动很大

2020年7月4日09点24分

lv.1-lv.2-lv.3多尺度模型仿真

项目	情况
循环数	200
磁体$dt$	0.25s
每个循环所使用的时间	240s
计算实况
循环开始时间	2020年7月3日23点24分
预计循环结束时间	2020年7月4日13点44分
计算状况	正常

lv.2-lv.3多尺度模型仿真

项目	情况
循环数	1200
磁体$dt$	0.25s
每个循环所使用的时间	7.5s
计算实况
循环结束时间	2020年7月4日04点19分59秒
计算状况	正常
数据文件	record_20200703_222342.mat

发现问题

这个地方的常数项已经除了一个dt，又另外除了一个dt

计算200个循环先

预计运算时间12h，完成时间12点

二级模型

三级模型的自感是错的，那这个是怎么算出来的？

说明矩阵比较小的话，互感矩阵不对称也能算？
数据文件record_20200703_160250.mat

采用新的lv.3自感矩阵进行二级模型计算

2020年7月3日20点07分

尝试去除lv.3的互感影响

只保留垂直场影响

2020年7月3日17点23分
对比二级模型的结果和混合模型的结果，推测是三级模型对一级模型的影响出现问题，可能是三级模型的互感，可能是三级模型的垂直场

检查Mutual_Inductance_3_1的问题

没有问题

经过求和之后，发现Mutual_Inductance_3_1与Mutual_Inductance_3_2的第一项没有10%以上的差别

第二步是将Mutual_Inductance_3_1全部归零然后计算

• todo
  
  归零Mutual_Inductance_3_1并不能解决问题
  
  第三步是将一级模型的垂直场计算也归零
  
  也不行

去掉lv.3 重新计算混合模型

问题

垂直磁场的计算出现问题

解决掉

三级模型的自感矩阵

2020年7月3日13点42分

排查问题

lv.2模型

二级模型拓展至40个单饼没有问题

加上lv.3的互感

感觉没有什么影响

加上lv.3的垂直场

另外将新计算的正确lv.2垂直场加进来

没问题，开始1200个循环
16*1200/3600 = 5.33h

2020年7月3日08点39分

电流计算出现问题

推测是互感矩阵出现问题

双绕单饼与lv.2单饼之间的互感出现负值：

与lv.1之间的互感也出现负值

检查问题

3-2的互感和3-1的互感都不对，采用椭圆积分的方式重新计算

解决互感问题之后依然存在奇异性问题

推测是方程结构问题，先搞一个简单模型试试

2020年7月2日21点14分

问题

调试过程中发现一个问题：前面计算的lv.3与lv.2模型之间的互感包括了一级模型，在计算中应当舍去

调试成功

奇异性

三级自感有问题

2020年7月2日20点17分

电流控制

2020年7月2日12点54分
开始三级多尺度程序

问题

三级模型的互感矩阵出错

原来是双绕单饼的自感计算错误，改正

修复完成

出错

三级模型与以及模型之间的互感计算出错


更正

出错

3-2 inner互感没有数值

2020年7月1日19点29分

将三级模型融入多尺度模型当中

三级模型忽略环向电阻，只支持径向电阻和电感
那么其固有方程就非常简单：
$$\frac{{d{I_c}}}{{dt}} \cdot L = {R_r} \cdot (I - {I_c})$$
即：
$$\frac{{d{I_c}}}{{dt}} \cdot L + {R_r} \cdot {I_c} = {R_r} \cdot I$$
接下来就是确定三级模型的径向电阻
径向电阻率：
$$
\rho = \frac{59.8}{56} \times 6.546178680702746\times {10}^{-10} {{\Omega} \cdot {{m}^{2}}}
$$

2020年6月30日08点59分

垂直磁场函数写到一般发现可能之前的二级模型垂直磁场计算函数出错了。无脑的将垂直磁场积分么，没有考虑环形电流上各个位置的电流元产生的垂直磁场方向不同的因素.

解决方式是：在积分公式的垂直磁场端乘以cos(α)

2020年6月25日15点01分

双绕线圈自感的计算和双绕线圈与外层线圈之间互感的计算没有问题，但是双绕线圈之间的互感计算出现问题
一方面是下面的四个单饼的互感计算出现问题，另一方面是自感计算出现问题

三级模型的自感、互感矩阵函数编写完毕

付诸计算。
在A分区

2020年6月24日13点51分

三级模型数据准备

1. 三级模型之间的互感
2. 三级模型与一级模型之间的互感
3. 三级模型与二级模型之间的互感
4. 三级模型造成的中心磁场
5. 三级模型造成的三种垂直磁场
6. 二级模型在三级模型的位置产生的垂直磁场
7. 电压

外侧单饼典型参数

函数文件single_pancake_parameter_outter.m

中心磁场

• 双绕线圈产生的中心磁场
• 外侧双饼产生的

互感

问题

单饼与单饼之间的间距应当为0.67，但是很多位置的计算并没有一次为准，后面的计算中应当改正。

2020年6月23日15点46分
A区的超算可以32核心并行计算

2020年6月22日16点46分

计划是将三级模型的状态调整好

内层24 (4个双绕的)外层36(6,7,8)
需要将基础数据的维度增加到50

基础数据

1. 中心磁场
2. 1-2互感
3. 2-2互感
4. 垂直磁场

中心磁场计算

原中心磁场数据大小，原中心磁场计算程序tool_level_2_Central_Magnet_field.m
新程序将磁场计算改为100

1-2互感

互感计算程序tool_level_3_1_Mutual_inductance_Matrix.mat
计算完成之后将结果加起来就是
循环次数改为50
需要后处理

计算中

互感计算程序tool_level_2_1_Mutual_inductance_Matrix.mat
预计计算时间34小时
开始计算时间：2020年6月22日21点58分
3. 2-2互感
tool_level_2_2_Mutual_inductance_Matrix
本身就是100层

4. 垂直磁场
   本身就是60层

2级模型

设计一个十小时的计算过程
14400个循环 电流40A/0.01 dt = 0.25s

2020年6月12日10点24分

数据处理

数据文件

record_20200611_102930.mat

计算时长

项目	图像	说明
控制电流		40s从0A增加到0.4A，保持80s
总电压变化		正常
总磁场变化

新的仿真

电流过程

40s从0A增加到0.4A，保持80s
预计计算时长21小时

2020年6月11日10点09分

数据处理

多尺度模型 数据文件record_20200610_172437.mat 二级模型 数据文件record_20200611.mat
20个单饼 dt = 0.2s I/t = 0.01A/s

项目	图像	说明
控制电流		40s从0A增加到0.4A
总电压变化		与二级模型基本一致
总磁场变化		多尺度模型的磁场比二级模型的磁场更低
多尺度模型磁场与二级模型磁场的比率		逐渐接近1

2020年6月11日09点17分

数据处理

二级模型，20个单饼，数据文件record_20200610_171802.mat

项目	图像	说明
控制电流		3000s从0A增加到30A
总电压变化		尾部略微上翘
总磁场变化		正常
时间终点1000s的温度		两侧的双饼温度最高
时间终点1000s温度最高的点		133/333不是最中间的匝温度最高
2000s时温度		中间的单饼温度最高
2000s时温度最高的点		177/333 177/333
1000s时的温度		在远离临界电流的地方，充电时温度中间高
1000s时温度最高的点		177.5/333
端部单饼最高温度变化

2020年6月11日08点31分

准备数据处理

1. 二级模型

数据文件record_20200610_171802.mat

2. 多尺度模型

数据文件record_20200610_172437.mat

3. 将二级模型的1:200点的数据分离开

数据文件record_20200611.mat

二级20单饼模型仿真

总循环次数30000(估计不能等到循环完成)
每次循环时间 2.5s
电流速度 0.1A/s
2020年6月10日13点52分
有点那个意思了

忘了速度太快超过临界电流

数据文件record_20200610_124245.mat
将电流上升速率减小到0.01A/s试试，dt变为0.2s，电流上限30A，也就是3000s,15000个循环，

宏观参数

20个单饼总自感: L = 1.50506188826080

20个单饼总径向电阻:0.00487367794731242

恒定电压应当为L*dI/dt

推测为电压计算程序出现问题，改进

二级20单饼模型仿真

控制电流I = 0.1t
dt = 0.1s
t1 = 30s
t2 = 60s

尝试将图像表现添加进程序里面去

二级20单饼模型
不考虑环向电阻
数据文件record_20200609_231721.mat

看起来很正常

终点电流也很正常

考虑环向电阻
电压变化

磁场

看起来很正常
60s电流

60s温度 稍微上升

60s环向电阻

分析

在二级模型没有问题的情况下，由于一级模型和二级模型之间的耦合很小出现问题的只有可能是：

1. 一级模型和二级模型之间的互感数值出错
2. 方程构成出现问题

检查

很明显，互感大小不对
X应当比Y大约小，约为Y的1/36

查看原因

可能是因为二级模型互感计算中，源电流和目标电流积分初始点和终末点的设定中出现了问题，多除了A

乘36^2数量级一致了

修复

修复完成，再来计算看看

处理数据

数据文件record_20200608_125550.mat

计算出来的β饼的环向电流是负的，随着时间的增长，环向电流越来越趋向于负值

1. 检查程序
2. 锚定最内侧环向电流
3. 完全使用粗糙模型进行仿真看看

数据处理

数据文件record_20200605_075639.mat

项目	图案	详情
控制电流		是设计值
电压		不应该失超的，但是失超过程倒是挺正常
中心磁场		不正确
温度		温度值低于环境温度，说明计算出错了

按照之前的计算来看，初始电流计算出来的温度值与此处仿真出来的温度值不一致，应该是改程序出错

上下表面的散热去除的时候只考虑了常数项，没有考虑系数项，所以出错了

2020年6月6日15点22分
计算完成，但是后期矩阵奇异，应该是中间的计算出了问题

数据文件record_20200605_075639.mat 部分输出20200696.txt

2020年6月5日07点43分

上次的计算

每次循环时间 典型值140s
数据record_20200517_091038.mat
计算24小时24*3600/140 =617
设计一个600个循环的过程试试
电流上升速率0.1A/s dt = 0.1
t1 = 30s
t2 = 60s

2020年6月4日23点49分

解决二级温度计算问题

开始60个循环的计算，电流上升速率0.0053A/s

进行程序调试

2020年6月4日16点48分

解方程时间33s

解方程时间155s，很长，但是构成方程的时间不能接受

温度计算的方式如果采用二级模型的方式大概可以大幅降低构成方程的时间，如果依旧采取现在的方式，降低计算时间的努力可能无法取得成功
计算10个循环完成，数据文件record_20200604_183517.mat

写二级温度计算程序吧

2020年6月4日19点47分

1. 径向热阻
2. 只考虑内外向传热
3. 计算发热功率
4. 解方程计算温度

完成计算，径向热导 level_2_thermal_conductivity_matrix.mat

2020年6月2日15点16分

温度计算

1. 更新温度计算程序，将上下面的散热去掉
2. 增加二级温度计算程序
   经过考察发现不应该设立二级温度计算程序，应当将二级电流模型转化为一级电流模型之后在计算温度变化。
   其原因是二级传热程序很难模拟环向传热

应当迭代二级模型中的环向电流

Circle_Resistance_Matrix_2

2020年6月1日22点00分

方程构成

1. 事先把level_2_1互感矩阵变为二维矩阵，这些部分不用循环
2. 二级模型对应的方程部分需要循环完成
3. 垂直磁场的计算需要在每个循环内部完成，每个单饼对应的垂直磁场计算方式都有所不同

2020年6月1日14点30分

优化程序结构

• 粗糙模型之间的互感
  level_2_2_Mutual_inductance_Matrix
  放弃优化输入数据了

方程结构构成

电阻永久改变

二级模型之间产生的垂直磁场

需要写一个程序来计算，注意来自于上方的单饼的垂直磁场是负指
[引用]王亚辉, 任亚杰. 圆环电流产生的磁场[J]. 周口师范学院学报, 2006(05):63-65.

$${\text{d}}{B_ \bot } = \frac{{\mu IR}}{{4\pi }}\frac{x}{{{{\left( {{R^2} + {d^2} - 2Rd\cos \alpha + {x^2}} \right)}^{3/2}}}}{\text{d}}\alpha $$

二级模型产生的垂直场矩阵准备完成

2020年5月29日09点23分

发现了磁场计算矩阵的问题

磁场距离定的是5mm实际应当是2.5mm
将原本的磁场矩阵数据存history文件夹，命名为Double_pancake_Central_Magnet_field_Matrix_20200529.mat
更正之后磁场确实上升的

数据处理

record_20200529.mat

2020年5月27日09点19分

磁体任意位置的垂直磁场

5~100mm间距导致的平面磁场。
数据文件名level_2_1_Vertical_Magnet_field_Matrix.mat
其中：level_2_1_Vertical_Magnet_field_Matrix_X代表在目标点位置产生的X方向磁场计算矩阵；level_2_1_Vertical_Magnet_field_Matrix_Y代表代表在目标点位置产生的Y方向磁场计算矩阵Y
使用方法为，取出距离对应的这一层矩阵，直接乘源电流列向量，即可得到目标点位置的X、Y磁场列向量，将两个列向量取勾股数即为垂直磁场

互感矩阵

数据文件名level_2_1_Mutual_inductance_Matrix.mat

数据处理

record_20200521_175153.mat
降低临界电流
此时仿真的模型中，所有的径向电阻调整为原来的59.8/56，临界电流调整为51.019

项目	图案	详情
电压		比临界电流调整前强多了
磁场		另外做了一下归一化，有一点点偏差，但是主要问题应该是出在测量时的系数上面
分电压		讲道理不应该差别这么大的
分电流		中间一些匝数的电流非常一致，但是最外侧几匝的电流就不同，可能也是导致分电压不一致的原因吧，是由电路结构决定的

磁体整合

三重尺度结构

需要研究的面用精细结构，T*A个元素，与之对应的双饼另一一面用粗糙结构，T个元素，其他的单饼用电感、电阻、环向电阻的结构，只关心环向电流

具体结构

假设α面上面还有num_up个单饼，假设β面下面还有num_down个双饼

1. UP部分与DOWN部分各个单饼的自感、径向电阻
2. UP部分与α的互感，DOWN部分与α的互感，UP部分与β的互感，DOWN部分与β的互感
3. UP部分与DOWN部分各个单饼之间的互感

采用eval(['row_',str,'=row']);clear row的方式可以自动修改变量名，这样可以一次计算多个距离的互感

开始计算了
输出的是一个三维数组，表征5mm~100mm间距的单饼之间各个元素的互感
预计五天半计算完成

从另一个方向考虑，当前面临的问题不是环向电阻系数的问题，而是临界电流不准的问题
这样的话，在自感情况下，环向总电阻2.967327578223025e-05
对应的临界电流51.019
考察此时的温度和垂直磁场，找出此时的真正临界电流，由于此时的温度和垂直磁场太小
所以将此临界电流作为实际临界电流
$${R_{\text{c}}} = {10^{ - 5}} \cdot l \cdot {I^{(n - 1)}}/I{c^n}$$
$$I = \frac{{{R_r}}}{{{R_r} + {R_c}}} \cdot {I_0}$$
$${I_0} = \frac{{{R_r} + {R_c}}}{{{R_r}}} \cdot I$$
$${I_0} = \frac{{{R_r} + {{10}^{ - 5}} \cdot l \cdot {I^{(n - 1)}}/I{c^n}}}{{{R_r}}} \cdot I$$
$$U = {R_c} \cdot I = {10^{ - 5}} \cdot l \cdot {I^n}/I{c^n}$$
所以求n值不应该着眼于U和I0之间的关系，应该着眼于U和B之间的关系

$$U = 8 \cdot {10^{ - 29}} \cdot {I^{16.416}}$$
Ic = 34.8533，n = 16.416

数据处理-仿真数据

此时仿真的模型中，所有的径向电阻调整为原来的59.8/56，时间常数应当有相应的改变，环向电阻调整为原来的0.466441435179773倍
数据文件为record_20200520_140651.mat

项目	图案	详情
电压		电压相差巨大，说明环向电阻修正的方式不对，n值得变化没有考虑进去
磁场		磁场倒是越来越接近
分电压		感觉α面的时间常数过大，而β面的时间常数过小
分电流		100匝环向电流，修正之后二者的电流走势如此接近！说明道路正确

2020年5月20日10点23分

数据处理-临界电流测试

目标电流57A，等待稳定，理论上稳定电压应当是1.6mV，根据这个值调整环向电阻，另外这个环向电阻的值是对应59.8/56倍的径向电阻的，应当符合实际情况
还有2.3128个小时才能计算完毕
数据文件record_20200519_224248.mat计算时间比预期稍长

项目	图案	详情
电压变化		0.0032305809
磁场变化		0.582948227
初始磁场		0.654323608579067

稳定下来之后，径向电流为57*(1 - 0.582948227/0.654323608579067) = 6.217713523804790 A
此时的径向电阻为 0.0032305809/6.217713523804790 = 5.195769936378669e-04 欧姆
此时的环向电阻为 5.195769936378669e-04*6.217713523804790/(57 - 6.217713523804790) = 6.361629466042992e-05

而实际上 稳定电压应当是1.6e-3 V
实际上的径向电流是 1.6e-3/5.195769936378669e-04 = 3.079428110928181 A
实际上的环向电阻应当是 5.195769936378669e-04*3.079428110928181/(57-3.079428110928181) = 2.967327578223025e-05

所以，模型中的环向电阻应当乘系数2.967327578223025e-05/6.361629466042992e-05 = 0.466441435179773

三级单饼状态

项目	图案	详情
自感		0.00891612815453612
径向电阻		0.000260219590401145
环向电阻		l = 160m
互感		output = tool_level_3_1_Mutual_inductance_Matrix(height)

数据处理-仿真测试

此时仿真的模型中，所有的径向电阻调整为原来的59.8/56，时间常数应当有相应的改变

数据文件为record_20200519_091521.mat，总计算时间

项目	图案	详情
控制电流		没错
电压		总的来说，修正径向电阻之后更接近实测值，但是在稳定部分还是有微妙的差别，等修正环向电阻之后再看看情况
磁场		也是更好了，这个差别应当是测量探头的系数不对造成的
分区电压		粗糙模型的分区电压反而下降了，这可能是互感导致的，也说明二者的平衡非常微妙
分区电流		二者的环向电流都有所上升

发现对称模型的问题，时间常数和临界电流时的电压都要重新计算

后来发现错有错着，断电仿真不用重做
另外，从作物的计算可以估测，从57A断电的时间常数为50.56秒，比从5A断电的时间常数更小，符合预期

临界电流测试状态

项目	图案	详情
目标电流		57A
时间间隔		0.001~1s变化
循环次数		1051
预计计算时间		22小时
目标电压		1.6mV 160m

2020年5月19日08点15分

数据处理-仿真测试

此时仿真的模型中，惊喜模型的径向电阻调整为原来的59.8/54.5.但其实按照计算，应当把精细模型的电阻调整为59.8/56，把粗糙模型的电阻调整为55.2/56.先看看增加精细模型的时间常数之后，精细模型的电压变化是不是更加接近实测值了？

数据文件为record_20200518_115737.mat，总计算时间

项目	图案	详情
控制电流		没错
总电压		有效，继续调整
总磁场		有上升，但是预计不能调整到完全符合实测
α电压		下降得更快了，合理
β电压		上升了
分区电流		合理

接下来将精细模型和粗糙模型的电阻都调整到59.8/56，再进行仿真

2020年5月18日11点05分
现在面临的情况是：精细模型和粗糙模型的时间常数都需要调整
先调整精细模型，同时调整环向电阻系数

计划

1. 将精细模型的径向电阻调整为原本的59.8/54.5（增加），进行多尺度模型的仿真
2. 在调整镜像电阻的前提下，仿真对称模型在临界电流(57A)的稳定电压值,以1mV为目标进行系数调整

临界电流测试状态

项目	图案	详情
目标电流		57A
时间间隔		0.001~1s变化
循环次数		1051
预计计算时间		22小时
目标电压		1.6mV 160m

仿真测试

项目	图案	详情
目标电流		60A,0.53A/s
时间间隔		0.25
循环次数		1000
预计计算时间		13个小时

2020年5月18日10点26分

数据处理

仿真实验，电流I = 0.53t，数据文件record_20200517_211934.mat，模型为多尺度模型，dt = 0.25s，磁体时长250s

项目	图案	说明
控制电流		没错
总电压		仿真电压比实测值小，这与断电实验中时间常数更长的结果相符，可能需要将精细模型的径向电阻设计得更大才行
总磁场		将惊喜模型的径向电阻增大看看
分区电压		符合预期
分区电流		符合预期

2020年5月18日09点01分

数据处理

断电实验，电流5A，数据文件record_20200517_183743.mat 模型为对称模型

项目	图案	说明
B0		B0 = 0.057397
B,V		走势正常
B时间常数		时间常数为59.8，比实测的54.5要大，这可能是因为径向电阻在精细模型中比在粗糙模型中的效果要更小一些
V时间常数		和B的时间常数一致

数据处理

再计算方程错误的情况下，利用拟合系数将自感调整到正常
仿真数据：record_20200517_105851.mat 实验数据：experimental_data_num49.mat 参数数据experimental_data_num49.mat0.53A/s的电流增加

项目	图案	说明
电压
磁场
分电压		错误的方程决定的
分电流		100匝位置环向电流

2020年5月17日15点54分

找到问题了

基尔霍夫电压方程第一个方程的电阻没有乘进去

计算

一个是验证简化方程构成
一个是验证修改错误后的情况

沙盒+爆点
dt = 0.25
t = 60s
预计 60/0.25*45/3600 约等于3小时完成 ，现在是17点06分，预计20点20分完成
有一些步骤计算时间特别长，怀疑出现问题

另外再开一个时间间隔更小的，dt = 0.1s ,预计10个小时完成

下一步计划

1. 时间延长
2. 时间间隔至0.25
3. 简化方程A的函数

只增加α面的自感，不增加β面的自感

计算过程中，虽然总磁场一直比测量磁场高，但是越来越接近，说明总时间常数还是太小。
对比实验数据发现非常接近了
只需要少量的修改电感值即可

α面的自感增加WRL.WRR.，β面的自感增加WRR.*

2020年5月17日09点11分

数据处理

record_20200516_232751.mat
将自感矩阵乘31.3237(54.5/27.45)，同时将径向电阻乘1.3237

项目	图案	说明
总电压与测量电压比较		数值差不多，但是时间常数明显不对，电感太大了
仿真磁场与测量磁场比较		数值差不多，但是时间常数明显不对，磁场上升太慢，电感太大

record_20200516_175914.mat

项目	图案	说明
总电压与测量电压比较
仿真磁场与测量磁场比较

数据分析

计算出来的磁场值比实测的磁场值大是正常现象，考察电压的值是否与实测值相同，考察磁场值走势是否合理

充电的时候环向电阻是电压源的一部分

径向电阻是耗电部件的一部分

待处理的数据

将自感矩阵乘1.3237*(54.5/27.45),同时将径向电阻乘1.3237，数据文件为：record_20200516_175914.mat
将自感矩阵乘31.3237(54.5/27.45)，同时将径向电阻乘1.3237，数据文件：record_20200516_232751.mat

对称模型 电感加倍 数据处理
α面电感增加到原来的(54.5/27.45)

项目	图案	说明
电压比较		说明走势对了，时间常数对了，只是电阻差了一些
磁场比较		等将电阻加上再来

电压值差了多少

按照这个倍数(1.323715465563159)再来
此时将L*(54.5/27.45)的计算结果保存为20200516.mat

• 对称模型的总互感是多少？
• 还有半个小时之后计算完成，计算完成之后开始新的计算，新的计算保留电阻和电感的增加，再将电感加2倍

使用经验公式计算出来的单饼自感

自己计算的自感

差不多

说明不是自感数值的问题
试试不同时间步长对于时间常数的影响

运用沙盒和爆点进行计算

1. 将电感系数调整为原本的1/10，能大大降低计算时间，预计时间常数2.5s
2. B=0.057397
   

时间间隔	图	说明
0.1		B=0.037738
0.05		B=0.037686
0.02		B=0.037654
0.01		B=0.037644
0.008		B=0.037629
0.005		B=0.037638
0.004		B=0.037637
0.003		B=0.03763
0.002		B=0.037635
0.001		B=0.037634

这说明时间间隔对计算结果影响不大

2020年5月16日10点07分

改变径向电阻获得改变

径向电阻减小到原来的(27.45/54.5)

项目	图案	说明
总电压与测量电压比较		明显不对
仿真磁场与测量磁场比较		时间常数还可以再大一点
α和β面电压比较		意料之中
α和β面环向电流比较		很合理

改变电感获得改变

α面电感增加到原来的(54.5/27.45)

项目	图案	说明
总电压与测量电压比较		电感还可以再大一点
仿真磁场与测量磁场比较		差不多，说明时间常数这样很合适
α和β面电压比较		α面的电压还是很低
α和β面环向电流比较		α面的电流还是很高

接下来的计划

利用增加电感的手法，尝试使用对称模型，看看效果

2020年5月15日20点51分
双饼模型径向电阻减小到原来的(27.45/54.5)
双饼模型环向电阻改变为原来的(27.45/54.5)*(1/0.7)
这是改变电阻方向的努力
record_20200515_230938.mat
另一个方向是改变电感
record_20200515_211821.mat
预计13个小时计算完成20200516-10:30

根据磁场计算出来的时间常数为27.45

更新对称模型的磁场计算程序

减小径向电阻到原来的一半

电压下降得厉害，磁场还是很大，怀疑磁场计算程序有问题
保存为V_0_5,B_0_5

增加径向电阻到原来的两倍

增加径向电阻会令电压和磁场都上升更陡峭，其中磁场的变化越来越明显

• 双饼的时间常数是54.5，故径向电阻应当上升55.2/54.5
  理论上来说：
• 断电冲击电压V = 2*2.274890645026072e-04*5 = 2.274890645026072e-03 V
• 时间常数电压为：8.368854992183333e-04 V
  仿真：
  断电冲击电压V = 2.6285e-3V,说明仿真模型的径向电阻至少为2.6285e-4欧姆，这个就是精细模型和粗糙模型之间的径向电阻差异的表现

2020年5月15日13点15分

时间常数开始计算

下周计划

• 完成径向电阻的计算
• 将两种模型的计算结果与实测结果进行对比
• 完善更多单饼的计算模型

2020年5月15日09点22分

数据处理-多尺度双饼模型仿真

项目	图案	说明
双饼电压		仿真值比实测值要稍微小一点
双饼磁场		仿真值比实测值要稍大一点
分模型电压		α面的电压上升比β面慢得多
分模型环向电流		α面环向电流上升更快
两种模型的自感		采用的是同一组数值

结论：出现电压分配不均的原因————精细模型中采用的电阻系数是以实测的时间常数和粗糙模型的电感和电路结构计算出的接触电阻率，并不适用于精细模型，精细模型的接触电阻率还需要另外计算。

为了测算精细模型中的接触电阻率，设计了新的仿真对象，一个对称的双饼模型。认为双饼的两面电流完全相同，这样只需在原单饼的基础上考虑两面之间的互感、垂直场即可计算出双饼中的电流。此模型的劣势在于拓展性差，必须保证双饼环境对称。

数据处理-精细模型

项目	图案	说明
电压
磁场

电压比实测值小，磁场比实测值大，典型的时间常数错误的特征

校正精细模型的时间常数的方案，利用对称模型做短路仿真，对比实测时间常数调整径向电阻

2020年5月14日22点19分

• 根据49系列的计算结果画图
• 新的互感矩阵计算出来以后尝试对称模型
  多尺度双饼模型仿真数据(1)：record_20200514_120804.mat
  临界电流稳定仿真数据:record_20200513_124444.mat

2020年5月14日15点09分
试试对称模型，调试一下

从对称模型的计算情况来看，出现问题的不是对称模型中的环向电阻的值，而是径向电阻比实际值大了。
所以尝试将镜像电阻减小到原来的1/2.63，看看情况
已经计算完成的部分命名为：record_20200514_155752.mat

接下来进行镜像电阻减小的测试
2020年5月14日19点19分 开始仿真
不行，减小径向电阻的同时，电压也变小了

判断是自感太小的原因

我傻了，计算互感的时候间距设置错误，设置成了5m ，所以总自感小了许多

2020年5月14日11点09分
实测在动态变化中0.5s的时间间隔太长了

2020年5月14日09点50分

数据处理

数据说明

首先给双饼环向电流中通45.62A的电流，等待环向电流与径向电流平衡

项目	图案	说明
双饼总电压		应当为1mV，根据这个变化调整环向电阻系数
双饼总磁场		比实测值小，是因为粗糙模型的电流小了
单饼电压		应当为0.5mV
单饼磁场		实测值5.33/2
稳定时间		I = 45.62A 稳定时间t = 156.8A

调整

1. 由于系统性的误差，双饼的环向电阻减小到原本的96.55%
2. 由于系统性误差，精细模型的环向电阻增加到原来的2.63倍

2020年5月13日18点33分

1. 根据45.62A的数据分析出模型中的环向电阻系数
2. 根据手头的数据计算双饼的临界电流：Ic = 56.996
3. 根据电流数据设计控制电流方案 I = 0.53t + 0.1965
4. 根据控制电流方案设计时间间隔方案

数据处理

α面的环向电流异常变化，原因是模型中的环向电阻计算错误

正在更正
看起来正常多了

试试dt = 0.5 ln = 100

成功了！

仿真 I = 45.62A t = 3706.1s 预计计算时间16个小时

数据处理

1. 200过后的数据就不对了，应该是时间间隔突变导致的结果
2. 并没有出现复数，不用取真值
3. 电流本身太小，而时间变化太剧烈导致的，所以不能进行阶跃式的时间间隔变化，特别是电流本身很小的时候
4. 做一个断电实验看看

2020年5月12日11点44分
奇异性问题依然存在，试试将beta面的第一匝化为i0

再试试将时间间隔调为0.01看看

时间间隔0.01就没毛病，说明电压、电流变化如果与时间间隔不匹配就会出现奇异性问题

计算400个循环，实际磁体时间4s，预计完成时间220分钟 16:30

还是会矩阵奇异，试试更小的电流？

试试放弃耦合？

发现一个严重问题：除dt的部分没有全部除

去掉[1,2]仅保留[1,1],[2,1],[2,2]结果不正确

去掉[2,1]仅保留[1,1],[2,2]结果正确

去掉[2,1]仅保留[1,1],[2,2],[1,2]结果正常，推测是没有锚定某一匝为总电流

看起来是B_equation错了

设计仿真过程

1. 去掉设计的坏点，临界电流统一为45.62A
2. 电流从0A开始
3. 选取几个点不断逼近45.62A
4. 速度0.1A每秒
5. 总电压和中心磁场计算程序

计算时间有点问题

电压计算程序出现问题，

磁场计算程序有没有问题,

方程解出来是个复数

准备不从0开始，从0.1A开始，也符合实际情况
这可能也是解方程时间很长的原因吧

这是直接取实部的结果
左磁场右电压

为啥磁场是负的？
电流也有一些是负的，不对劲

初始化电流0.1A，计算时间正常多了

左磁场右电压

beta面的电流

待稳定，可能得采取第一匝电流为环向电流的措施

先算500个循环试试

矩阵为奇异值了，两种可能性：

1. 电流解出来出现复数
2. beta面的控制电流未控制
3. 时间跨度变化过于剧烈
   接下来做一个断电仿真试试看
   
   500个循环，164s

2020年5月11日13点04分
I2J函数有一些问题
X_Bbeta写成了XBbata
criecle_resistance_matrix没有赋予初始值
A面的方程出来了
[2,1]位置的方程(84行)，电流区间出错
A面的径向电流和B面的电压没有什么关系
86行，不能用end，最好用实际的矩阵位置
第一个看起来没有问题，可以开始设置控制电流了！

尝试使用对称的思路来解决问题？

2020年5月8日18点48分

粗糙模型的第一匝环向电流不再为控制电流

2020年5月8日10点50分

将精细模型的方程构成改为函数

2020年5月7日20点43分

重构中心磁场计算矩阵和垂直场计算矩阵

tool_Double_pancake_Central_Magnet_field_Matrix.m 问题：双饼的中心磁场方向和单饼中心磁场方向不同
[X_B,Y_B,Z_B] = tool_self_Vertical_Magnet_field_Matrix(distance)
注意垂直场计算需要把β面的电流变为[2TA - A,1]的矩阵来计算

双饼总电压计算矩阵

2020年5月6日10点15分

失超

项目	图案	说明
输入电流
电压
磁场

存档 record_20200506.mat

计划

• 将双饼中另一个单饼的影响加入计算当中
  1. 方程个数增加T个
  2. 需要计算β面每匝和α面每个元素之间的互感
• αβ两面之间互感的正负参考α面元素之间互感的正负
• 需要计算β面每个匝数之间的互感
• 需要计算β面每个匝数之间的电阻
  6. 需要计算β面每匝的环向电阻
• 需要计算β面每匝的自感
  8. 先把β面的方程列出来，然后进行方程耦合
• 同向的互感表现为正

粗糙模型没有径向电流的计算！

恶劣条件下的充电情况

初步数据处理

1. 将温度变化变为视频
2. 电流变化
   项目|图案|说明
   :-:-:-:
   输入电流||与之前相同
   输出电流||
   时间终点温度||很高了

接下来计算恶劣条件下失超过程，从2856点开始进行大电流输入

2020年5月1日20点06分

处理数据

项目	图案	说明
输入电流		设定的电流情况
最外侧一点的环向电流
输入30A电流时实际的最外侧环向电流		1.环向电流在不同匝数分布不均；2.一些电流径向输出
临界电流32A点的环向电流		明显有电流变化
临界电流32A点的径向向电流		对于每个点来说，环向电流与径向电流的和并不等于总电流
总电压		已经进入失超曲线了
磁场		随电压变化
(150,7)温度变化		液氮沸点76.59K
原理此点的(300，1)温度变化		很小
输入30A，等待400s之后的温度分布		明显看到坏点的温度更高，其他位置温度呈环状分布
t = 596s，Iin = 49.6A时的温度分布		内侧温度升高，但是还没有进入失超阶段

接下来的数据处理

1. 温度变化动画

close all;clear all;clc;x =
linspace(0,2*pi,201);k = linspace(1,20,20);for idx = 1:length(k) plot(x,sin(k(idx)*x),'r','LineWidth',2); grid on ylim([-1 1]); %
时为了自己预先查看用的，用延时来控制matlab绘制速度endmovie2avi(M,'test.avi','compression','None','FPS',5);
%
这里选择无压缩方式<'compression','None'>;播放帧速<'FPS',5>
5fps

2. 更多点的温度变化
3. 在撒热条件不好的情况下会发生什么状况？

2020年4月29日13点31分
准备进行新一轮运算


输入电流走势最重点49.6A

2020年4月29日09点46分

• 搞定磁场影响临界电流
  在4.2K lgB 与 lgI 是直线关系
  在77.3K lgB 与 lgI 是曲线关系
  B|I|lgB|lgI|
  :-:-:-:-:
  1|55
  2|29
  4|8.5
  6|1.8
  6.4|1
  $$
  I_{c} = I_{c0}*e^{-0.73\times B}
  $$

• 搞定温度影响临界电流
  :-:-:
  T|I*e^-0.73
  4.2|1800
  10|1400
  20|1100
  30|845
  65|200
  77.3|55
  $$
  I_{c} = I_{c0}*e^{-0.04\times T}
  $$

绝对零度 -273.15°C = 0K
液氮温度 -196.56°C = 76.59K
$$
I_{cB,T} = I_{c76.59}\times e^{-0.73B}\times e^{-0.04(T - 76.59)}
$$

2020年4月28日10点15分
计算结束时间 8:32:50

没有解决几幅图共用colorbar的问题

用savecaxis = caxis caxis(savecaxis)命令可以统一colorbar

2020年4月27日21点14分
79.6A以后的恶劣条件温度统统很高，不具有代表性，但确实在升高

计算用时

超算计算用时6.5s

开始计算温度变化：1~2856

开始时间【2020年4月27日22点03分】
计划用时11小时

2020年4月27日11点54分

尝试用解方程的方式计算温度

由于每个节点的热容非常小，每个点的温度和功率应当是平衡的，即自己产生的功率加上从周边点吸收的功率的和为0

• 构建六向流入热导矩阵 Six_direction_inflow_thermal_conductivity_matrix
• 用循环方式观察方程构成
• 将循环构成方程的方式改为矩阵运算构成方程的方式
• 完成温度计算函数

不采用稀疏矩阵的情况下

构成方程11.5s
计算时间55s
图像正常

尝试使用稀疏矩阵

构成方程12s
计算用时61.4s 而且算错了

散热条件恶劣

散热条件良好

2020年4月25日10点05分

可以用发热功率代替温度来表示当前状态

某处的温差是向内所有的功率造成的温差，取和之后再计算即可

计算结果

项目	图案	说明
输入电流		正常
电压		上升正常
输出环向电流		问题：最外侧一匝的环向电流不对
磁场		持续上升，此时已经失超了
功率图像		632s
发热功率数值		632s
充点过程中的环向和径向电流		分布不均匀

2020年4月24日19点27分
D区计算完成时间：
A区计算完成时间：
符合预期，两个结果文件大小一样看起来计算结果一致
出错！ 时间间隔设置错误！
重算！ dt = 0.02 N = 1800 预计时间1800 × 24/3600 = 12小时 预计磁场时间 1800×0.02 = 36秒 预计磁场时间终点 632s

2020年4月24日18点16分

项目	图案	说明
(150，7)温度变化		突变的位置为时间间隔突变导致
596s时间点温度分布		问题挺大的
最开始的温度分布		还是能看到特征点的温度比较高.推测是因为温度变化太小而功率太大，所以应该减小迭代系数
IC = 10e-5 n = 100		看看
IC = 10e-5 n = 1000		再看
IC = 10e-7 n = 100		貌似过头了
IC = 10e-6 n = 100		看起来很典型
IC = 10e-6 n = 200		没啥区别
IC = 5*10e-7 n = 100		有点意思
IC = 3*10e-7 n = 100		只是针对这种情况，由于功率太小而温度变化太大导致不收敛的问题
IC = 3*10e-7 n = 500		有明显变化，说明500次迭代不够
IC = 3*10e-7 n = 10000		说明各个位置的温度收敛特性不同，不能一概而论，设想在迭代过程中改变迭代系数

2020年4月23日21点12分
结果分析

项目	图案	说明
输入电流		最内侧节点
输出电流		电流明显变化
电流放大		最外侧
电流再放大		推测是径向电阻太大导致模型失效
电压		总电压
初始电压		0.29mV
电压上升过程		5.6mV
失效过程
不可见过程		电压是由径向电流算出来的
磁场过程
磁场无效化		磁场由环向电流计算出来的
选定时间节点		596s，节点2856
596s环向和径向电流		明显有充电特征
411s,1006		注意临界电流更低的点

温度可视化

示意图

节点2856处的温度

可以看到整体明显上升

接下来从找出的节点开始计算即可

当我们讨论失超的时候，我们在讨论什么

1. 将临界电流条件设置得更加符合现实
2. 将散热条件中的上下表面散热去掉，上下表面散热条件很差
3. 温度的过程可以后面再算

全新临界电流

全新电流过程

30A保持400秒，1/0.01 + 3/0.03 + 10/0.1 + 50/0.5 + (400-50-10-3-1)=736
开始以0.1A/s的速率上升到80A：(80-30)/0.1 = 500s
1/0.01 + 3/0.03 + 496/0.1=5160
总的循环次数
5160+736=5896

2020年4月20日11点28分

数据处理

1. (150,7)位置温度变化
2. 总电压变化
3. 输入电流
4. (150,7)径向电流
5. 终点径向电流
6. 终点环向电流
7. 33.1400s各个节点总电流

环向电流异常变化的原因是什么？

原来是画图出错了，内径比设计值要小
解决问题,reshape变为两行两列

环向电流和径向电流

计划将图形窗口分块也写入可视化函数

完成！

2020年4月17日18点38分
停止A区的计算，下次可以接着计算，即使特征变化了也可以用

进行磁场和电压计算
保存为record_20200417.mat

项目	图案	说明
电流		I-t图像
电压		中断于140.91s
中心磁场		环向电流变化较小
温度		(150,7)节点
径向电流		2000位置
环向电流		2000位置

2020年4月16日21点36分
尝试36份
预估计算准备一个半小时
11点开始计算
实际计算时间

一个循环18s

一共6400循环，6400*18.2/3600 = 33小时
尝试使用A分区的机器 时间35s更长

计算开始时间 23:25 对应第八次循环
24:05 对应105循环
每小时146循环，每次循环24.66s

时间24+7:09，对应1115个循环，也就是一个小时146个循环，即43.83个小时

2020年4月16日18点26分

• 进行计算准备
  33个节点的互感计算，花费时间39.52秒，一共333*72 = 23976个节点，预计共花费时间8个小时，实际花费时间5小时
  读取所需要的数据所花的时间：
  
  一个4GB的数据花费59s
  两个8GB的数据花费一共200s
  解一个方程需要的时间是105s
  
  看看不计算温度和磁场的条件下一个循环需要多少时间：135s
  
  说明构成方程的时间是50s？
  看看计算磁场和温度的条件下一个循环需要多少时间：137s
  
  几乎没有变化
  需要改变思路，用更少的每匝分解个数

20个循环需要多长时间计算

2020年4月15日21点21分

• 增加细密度

增加计算的细密度

• 总结全部计算流程
• 进行计算准备
• 计算调试

计算流程

1. 确定基础设置与环境变量
   设置函数包括： 单饼属性single_pancake_parameter.m；接触热阻Thermal_contact_resistance.m；材料的物理属性Thermophysical_Properties_of_Material.m；环境温度External_temperature.m
2. 进行计算准备
   需要用到的计算数据主要有：互感矩阵tools\Single_pancake_Mutual_inductance_Matrix.m；径向电阻参数tools\Single_pancake_Radial_resistance_Matrix.m；自场垂直分量计算矩阵tools\tool_self_Vertical_Magnet_field_Matrix.m；单饼中心磁场计算矩阵tools\tool_Single_pancake_Central_Magnet_field_Matrix.m
3. 设定电流过程
   设定电流过程用到的子程序主要有：电流控制fun_Current_Control.m；时间间隔控制fun_Time_Interval_Control.m
4. 导入准备好的数据并开始计算
   计算过程中用到的子程序主要有：电流发热fun_Current_Heat.m；温度变化fun_Temperature_change.m；温度影响环向电阻fun_Circle_Resistance_Matrix
5. 记录数据
   记录数据用到的子程序主要有：电压记录fun_Voltage_Single_pancake.m
6. 数据处理
   数据处理用到的子程序主要有：电流可视化fun_Current_Visualization.m

2020年4月15日07点25分

• 温度模块调试
  
  以1883为例调试
  
  推测原因是温度变化只考虑上下散热而不考虑其他位置的散热，其实内外散热条件比上下散热条件更好
  总功率变化
  
  加上其他方向的1K功率之后，温度几乎没有变化了
  温度变化（迭代6次）:
  
  温度变化（迭代12次）：
  
  温度变化（迭代1次）：
  
  温度变化（迭代100次）：
  
  实践证明迭代次数对计算时间的影响比较小，总计算时间大约从220s至500s不等

2020年4月10日10点13分

电流变化

电压变化

环向电阻影响时间常数，一个坏点如何影响双饼的整体电压电流特性呢？
时间常数tao = L/(R1+R2)。随着环向电阻的升高，单饼的时间常数变小

中心磁场变化

关注节点环向电流变化

关注节点径向电流变化

300s时候的径向电流

300s的时候某一位置(1:15:end)的径向电流

300s环向电流

300s的时候某一位置(7:15:end)的径向电流

300s的时候某一位置(1:15:end)的径向电流

(4:15:end)径向电流

(11:15:end)径向电流

2020年4月9日14点20分

节点[150,7]临界电流为45.62

其他结点的临界电流为100
重点关注节点[149,7][150,7][151,7][150,6][150,8][150,15][150,1]
注意节点[150,7]节点为由内向外，第151匝，第7节点

时间控制电流

2020年4月8日19点57分
中心磁场变化

总电压变化

输入电流变化

温度不行

最终的环向电流

最终的径向电流

节点[150,7]的环向电流和径向电流

节点[0,15]的环向电流和径向电流

最外侧节点的幻像电流和径向电流

2020年4月7日08点53分

• 电流可视化visualization
• 临界电流区分
  
  
  2020年4月7日20点28分
  完成调试

2020年4月3日15点45分

计算3000号电流元处的垂直磁场

计算3000号电流元处的环向电流变化

2020年4月3日09点50分

垂直场与临界电流之间的关系：

$$y=117.2 x^{2}-166.6 x+78.38$$

2020年4月2日08点45分

• 耦合磁场
• 耦合温度

2020年4月1日17点33分

• 电流如何流过缺陷点
• 仿真失超过程

2020年4月1日16点57分

• 加快磁场计算速度，形成矩阵

• 协助计算电子偏转器

2020年3月27日09点11分

新一轮仿真

这次接近临界电流试试
从45A~50A， 每秒0.1A，一共50秒，每秒50次循环，一共2500次循环。
45A保持50秒，每秒10次循环，一共500次循环
47A保持50秒，每秒10次循环，一共500次循环
50A一直保持，前10秒每秒100次循环，一共1000次循环

过程

磁场运算7600秒，必须改进

电流变化

电压变化

磁场变化

B-V 变化

2020年3月26日13点52分

临界电流：45.62A
n值：7.69
判据：10uV/m
V = 10e-6.l.(I/45.62)^7.69
R = 10e-6.*l.*I.^6.69.*45.62.^7.69

2020年3月26日10点02分

磁场计算时间

计算两组磁场大约需要181秒，每组磁场大约需要90s

计算结果与之前的计算结果一致

算一个80步的结果出来，大约要120分钟

实际运行7504秒，是80秒时长的41.6倍，符合预期

2020年3月25日07点58分

今日计划

• 调试循环程序
• 中心磁场随电流变化函数
• 总电压随电流变化函数

电流过程

• 持续10ms的5A过程，之后是0A
  图片一

图片二

• 这说明电流运算没有问题们可以开始磁场函数和电压函数的编写

• 磁场计算函数运行速度150个循环10s
  

• 电压计算感觉不够精细
  
  

• 磁场变化
  
  
  0.35秒发生了什么？原来只计算了80步

2020年3月24日14点44分

• 电流过程
• 循环计算程序
• 形成充电、时间常数测量过程
• dt随时间变化
• 接近临界电流时环向电阻变化

2020年3月24日13点36分
下一步是构成循环

2020年3月24日11点01分

互感矩阵确实出现问题已解决

计算成功！

时间34s
100s总时间341001000=3.4e6s=944h

用超算计算很快

2020年3月24日08点35分
解方程矩阵奇异

1. 检查互感矩阵
2. 检查方程构成
3. 多尺度方程

2020年3月20日10点02分

解决矩阵奇异问题

矩阵奇异导致方程组无法解开

预期解决方法

1. 重新检查方程构成
2. 重构元素互感矩阵，特别注意互感正负
3. 尝试以di代替i，解出电流变化值，而非电流值

2020年3月19日16点12分

电路模型

2020年3月19日10点22分

双饼测试参数

参考电阻率70uΩ·m^2
$$
{70\times {10}^{-10}}{{\Omega} \cdot {{m}^{2}}}
$$

• 时间常数：55.2 s
• 自感：0.024826439479504 H/0.025143061116848 H

总径向电阻 = L/T = 4.497543383968163e-04 Ω/4.554902376240633e-04

径向电阻率

$$
\rho = 6.463743936476562\times {10}^{-10} {{\Omega} \cdot {{m}^{2}}}
$$
$$
\rho = 6.546178680702746\times {10}^{-10} {{\Omega} \cdot {{m}^{2}}}
$$

2020年3月19日09点26分

计划

• 径向电流电阻矩阵
• 通过短弧段电感矩阵计算电流变化

公式测试

$$
7.83\times {{10}^{-2}}{\Omega }\diagup{{{m}^{2}}}
$$
$$
7.83\times {{10}^{-2}}{{\Omega }/{m}^{2}}
$$

复制粘贴之后去掉头尾的[]和\然后隔行用$$包围起来即可

2020年3月19日08点21分

YBCO的径向电阻7.83uΩ/cm^2

即 7.83e-2 Ω/m^2

$
7.83\times {{10}^{-2}}{\Omega }\diagup{{{m}^{2}}};
$

2020年3月18日18点49分

等待各元素互感计算结果

从自感的对比来看，比例很均一为0.3809，这是由于计算方式导致的

总自感结果一致

从按匝排布的总互感对比来看，互感计算没有问题

2020年3月18日08点28分

垂直磁场函数计算时间

15份结果

20份结果

2020年3月17日11点04分

• 计算单饼线圈造成的任意位置的磁场
  笔记本内存不足

2020年3月16日10点18分

计划

• 计算单饼线圈造成的任意位置的磁场

• 形成短弧段电感矩阵

• 安装matlab

问题

直导线的自感阻碍电流增加？

回答

自感与互感的和应当为正，在计算中减去这个值与电流变化的乘积

2020年3月14日19点02分

组会收获

• 本地电流对本地磁场没有影响，所以计算磁场时去掉本地电流的影响
• 短弧段的自感用直线段的自感代替

2020年3月13日14点34分

SMM计算结果

分享文件: SMM.txt
链接地址：https://pan.cstcloud.cn/s/wj6eRYBORaY 过期时间：2020-03-20 14:30:49

2020年3月13日13点09分

组会

组会报告20200307...秦朗.pptx 提取密码：9CAY 过期时间：永久有效
组会代码：800712399

2020年3月12日17点31分

椭圆积分的参数为k^2,此处出错，必须大改

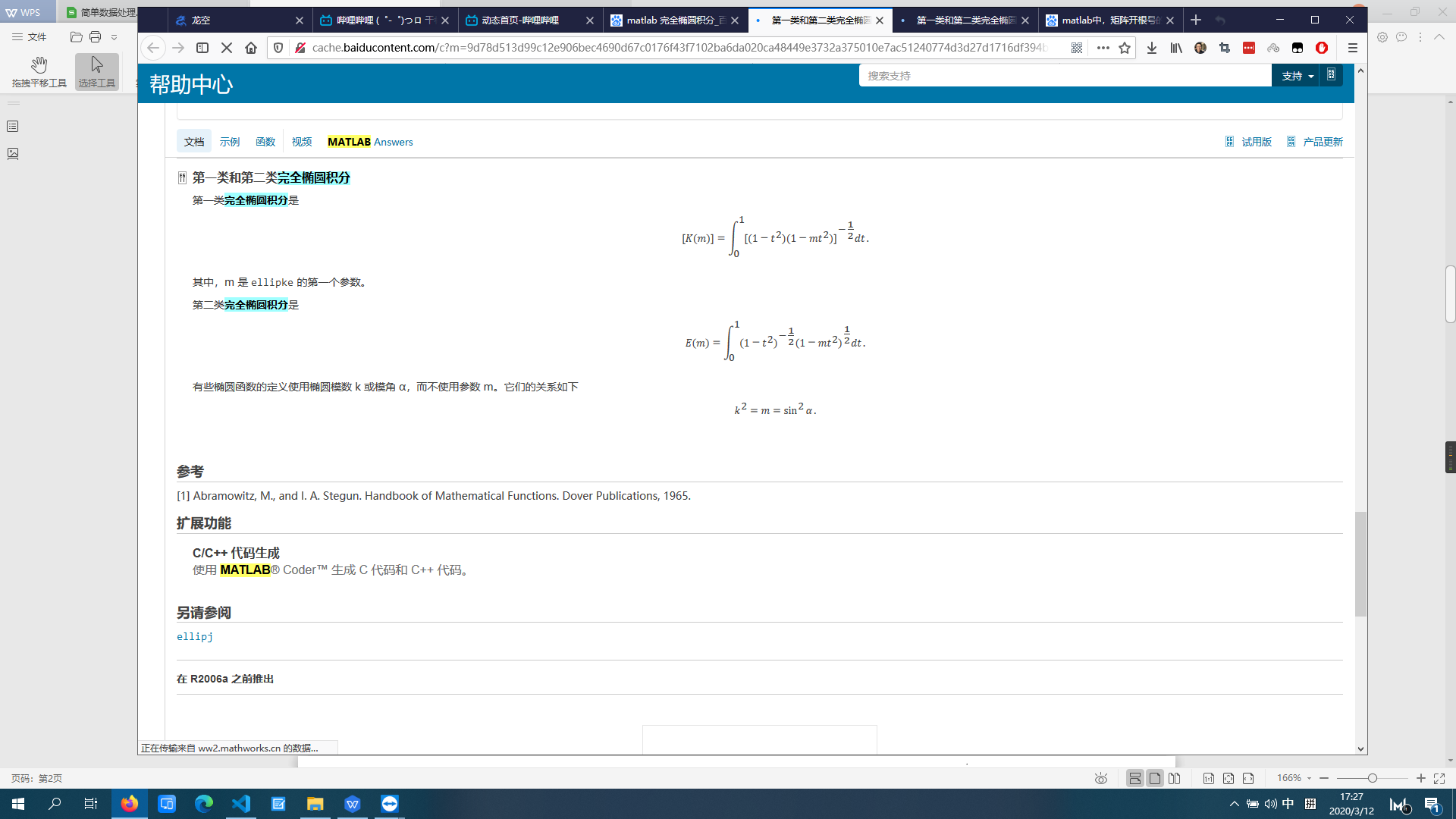
2020年3月11日10点06分

不同高度间距下的整匝之间的互感

不同高度下的弧线段之间的互感

21点19分

整个磁体的自感和互感没有计算

2020年3月9日18点49分

串联线圈的自感L=L1+L2+2M

多个线圈为矩阵元素的和

2020年3月9日11点05分

计划是首先计算中轴线上的磁场，然后计算空间任意位置的磁场，最后计算单饼内部的磁场

2020年3月6日10点45分

计算200A 10V的情况下上下表面散热功率和温度关系。

结论：散热良好的情况下，双饼平均温度比环境温度高2.28e-4K

2020年3月3日10点37分

通过计算得到每一个节点温度改变1K所需功率——即散热功率，对比此节点的输出功率，即可得到节点的温度改变值。而散热功率的一部分（在下一个循环中）会被计入周边节点的输入功率

2020年3月2日17点37分

接下来就是热量导致温度变化

2020年3月2日11点14分

改变了节点的位置模式，从两层之间改编为每匝中间，从而简化了矩阵构成

6面面积计算函数有待调试

是上传失误，函数没问题